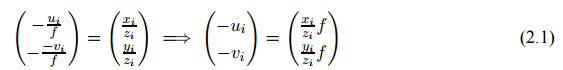How to debug garbage

I encounter several cases where the debugging infor gives me garbage like this

7f95d26c0000-7f95d26fd000 r-xp 00000000 08:05 5767281                    /lib/x86_64-linux-gnu/libpcre.so.3.13.1

It seems to be caused by wrong path, for example, there is dash (if there is space is ok). The path in windows is not always recognized by Ubantu. Correct the path format and this issue is solved. 

PCL pointer issue

I want to set a point cloud as a member of a class, and declare PointCloud::Ptr out_pcl_cloud; in the class definition. However, when I try to concatenate several point clouds together, it always gives me segmentation fault.

To solve this, declare a new pointer in the cpp file, PointCloud::Ptr cur_pcl_cloud (new PointCloud());, and use out_pcl_cloud = cur_pcl_cloud; to copy the point cloud data. Do not use *out_pcl_cloud = *cur_pcl_cloud; which appears to copy nothing.

To show all the pcl continuously, initialize the viewer by pcl::visualization::CloudViewer viewer( "viewer" );, and then viewer.showCloud( vo.out_pcl_cloud ); Do not use while( !viewer.wasStopped() ).

ROS rviz resource not found

I use the launch file to start rviz and encounter the problem of "resource not found". According to here and here, this is because ros cannot find the package location. To solve the problem, go to the catkin workspace directory and source devel/setup.bash, and then go back to where the launch file is located, such as the sub folder of the package, and roslaunch.

opencv中用optical flow检测运动物体

这里描述了一个简单的方法可以在图像中检测运动物体。首先在两张图像中运行optical flow, 然后找到homography。之后用perspectiveTransform把prevPts投影到warpedPts，比较warpedPts和nextPts就能找到运动的物体。如果物体不动，warpedPts和nextPts很接近，不过如果有运动它们之间的差就会很大。

一步步学习Visual odometry - Part2

有两种方式可以匹配两帧中的特征点，一是跟踪一个图像中的特征，适用于运动幅度较小的情况。二是在两张图像中分别检测特征点再进行匹配。为了去掉错误的匹配，可以用mutual consistency check和ratio test。不过ratio test需要根据经验设定阈值，所以不如用ransac来去掉outliers.

特征点的个数对结果有很大影响。一般特征点越多越好，而且要均匀分布在图像中，可以把图像分成网格，在每个格子中提取一定数目的特征点。对于640x480的图像，通常1000个特征点比较合适。

除了使用特征点，还可以用dense correspondence match。光流法可以跟踪全部的或者特定的像素，不过它假定运动很小，可能不适于VO。

用ransac去除outlier的时候，需要的内点越少所需要的iteration越少，时间也越少。所以尽可能的使得计算运动所需要的特征点数目比较小。不过如果特征点噪音很大，用更多的点会使得误差更加均匀分布，从而减小结果的误差。所以这时用8点算法可能好于5点算法。5点算法的code在opencv 3中有find essential mat函数，另外还有这里，这里。

一步步学习Visual odometry - Part1

在单目VO中，相机的运动和场景的3D结构都要从2D图像中获取。因为不知道绝对的距离，初始的两个相机之间的距离通常设为1.每当得到一个新的图像，相对的尺度和相机运动由已知的3D结构或者trifocal tensor得到。根据wiki，tensor是一个3x3x3的矩阵。trifocal tensor就是描述三帧之间关系的矩阵。

单目VO主要分为三类，基于特征点的方法，appearance based，和两者的混合。Nister第一次使用了VO这个词。跟之前方法不同的是，他们不是跟踪特征点，而是在每一帧里面单独检测Harris角点，然后进行匹配，这样就避免了跟踪过程中特征点的漂移。他们也不是用3D对3D的匹配，而是3D对2D的匹配，而且使用了5点算法和ransac去除outlier。还有一个是Milford提出的RatSLAM，用场景的中心做template tracking。

为了减小叠加相机姿态造成的轨迹漂移，通常在最近的m帧使用bundle adjustment优化，这个过程叫windowed BA。

在计算相机运动的时候，通过匹配特征点可以找到两帧之间的E矩阵。8点算法要求3D点不能都共面，而5点算法没有这个限制，它只需要相机标定。这里提到了Opencv中的findFundamentalMat使用了8点算法因此不是特别稳定，推荐使用5点算法。在该函数中有两个地方可以调整，一个是epipolar line的距离，一个是confidence level。根据这里，距离的设定是0.006 * maxVal。

在分解E矩阵的时候，可以得到四个可能的R，t。通过三角定位判断所有点是不是都在相机的前面，我们可以得到唯一解。这个解作为初始值再进行优化得到正确的R，t值。优化的过程就是减小反投影残差。

初始的两帧的运动确定之后，后续的尺度要以此为依据。前两帧的3D点对和对应的新的3D点对之间距离的比值就是尺度的比值。为了得到更准确的值，我们可以计算许多点的平均值或者中值。相应的，位移t也根据这个尺度调整。这里的特征点至少要在三帧中被跟踪和匹配。另外一种方法是用三帧之中特征点的trifocal constraint来计算尺度，不需要三角定位。

一步步学习Visual odometry - 综述

最近做视觉里程计visual odometry各种崩溃，只能使用一步步来的方法来梳理头绪。
Scaramuzza大神有关于VO很好的介绍，这里记录下学习笔记。
VO有几个基本假设。首先光照条件要充足，然后场景大部分要是静止的。图像中需要有足够的特征来提取运动。两帧之间的重叠要足够大。

VO最早用在火星车上面，后来被Nister发扬光大。它解决的问题是，一个相机在场景中运动，并记录下一系列图像，从这些图像中如何恢复出相机运动。把没两帧之间的运动相加，就可以得到一个完整的轨迹。我们也可以在过去的m帧上面运行iterative refinement来优化局部轨迹。

在VO中，运动估计是最重要的部分，它计算了相机从前一帧到当前帧的运动。我们可以用appearance based方法，直接用图像的像素值来匹配两帧图像。我们也可以用特征点来进行匹配。

如果两帧之间的匹配都是2D的点，至少需要5个点来恢复运动，点越多越好。通过这些对应点可以找到本质矩阵E，然后用SVD分解得到R和t。我们通过最小化反投影残差来找到真实的解。但是，我们并不知道在真实世界中相机移动的距离，只知道相机移动了一个单位。

如果我们既知道真实的3D点，又知道图像中对应的2D点，这就是PnP问题，至少需要3个点来解决，也是通过最小化反投影残差。在单目VO中，需要先从两帧之中通过三角定位得到3D点，然后跟第三帧的2D点匹配。

在三角定位中，如果相机移动的距离相比场景的深度很小，那么得到的3D点有很大的不确定性。为了避免这个情况，需要舍弃那些距离很近的帧，而是选取距离远的关键帧。选取的标准是3D点的不确定性很小。这一步是非常重要的，一定要在更新运动之前进行。

最后，在最近的m帧中要做bundle adjustment来优化轨迹。

在图像匹配时，会出现很多和运动不相符的outlier，我们必须把它们去掉。常用的方法是ransac。ransac不会给出确定的答案，所以不同时间的运行可能得到不同结果。当iteration增多时，得到的结果往往更稳定。最高效的方法是1点ransac，找到inlier后可以估算6DOF的运动。如果特征点的匹配有很大噪音，用更多的点的ransac会更准确。

为了优化VO的结果，通常需要上千个特征点，均匀分布在整个图像中。

How to extract data from ROS bag

Extracting image from ros bag can use call back function directly and save the image. To save the data in text file, such as the camera matrix, rosbag play and then use the following command according to this

rostopic echo -p /camera/camera_info > data.txt

If you want to save a lot of data, such as the information from imu, see here

in the bag directory, run

rostopic echo -p -b airground_rig_s3_2013-03-18_21-38-48.bag /imu/data >imu.csv

and then you can open imu.csv in matlab.

CV resources

I have found a good site here, which lists useful CV blogs and resources.

一步步学习SFM 五 Opencv multiple view geometry

之前做VO只能做到两帧之间对比的up to scale的版本，之后受到理论理解不深的限制很难再继续做优化之类的得到metric scale。看来还是需要好好先把理论搞清楚。正好看到了这本书，于是补一补基础知识。

分解F矩阵
两帧之中特征点和相机姿态的关系受到epipolar geometry的约束。通常假定第二个相机的姿态是相对第一个相机而言的，就是说第二个相机的旋转R和平移t都是相对第一个相机。两帧之中的特征点满足一个关系，叫做epipolar constrait，跟特征矩阵F有关。F又跟R和t有关。F的rank是2，determinant是0.也就是说相机的姿态可以从F中恢复，具体推导过程在这本书The essential and fundamental matrices这个章节。

假设一个3D点X在第一帧的投影是x1，在第二帧中的投影是x2，那么x1的位置使得x2只能在第二帧的一条线上，叫做epipolar line。F可以帮助在这条线上寻找x2的位置。所有的epipolar line都相交于一点，叫做epipole。

F是一个3x3的矩阵，不过尺度是不确定的，所以只需要有8个对应点就能计算F。如果特征点数目多于8个，就用least square找到误差最小的F。不过当8个点都在同一平面上的时候，这个方法不能使用。Opencv中的cv::findFundamentalMat函数还可以用7个点计算F，因为我们已经知道所有的epipolar line都交于一点，这个条件也限定了F。findFundamentalMat在用7点算法的时候可能返回3,因为这时可能有三个解。在8点算法，ransac, LMedS都只返回1或者0.检查findFundamentalMat的返回数很重要，因为有些时候点选取的不好，无法计算F。

这本书中提到了一个重要的问题，就是求解F的时候图像中对应点的选取非常关键。这些特征点需要在图像中均匀分布，并且包含不同深度的点。实际上可以用RANSAC来得到更准的F。首先用SURF寻找和描述特征点，再用knn matcher来找到两个最近的匹配点。如果最好匹配的距离比次好匹配的距离小很多，那么可以肯定最好匹配没有误差，否者说明最好和次好匹配很难区分，要去掉该特征点。接下来从图像A到B和图像B到A分别做匹配，只选取那些都是最好匹配的特征点。最后就是用RANSAC找到F和inlier。之前去掉错误匹配的过程是为了让ransca有个更好的初始条件，inlier更多就更容易得到准的F。

假如对应点都在同一个平面上，可以让它们的Z坐标都是0,那么3x4的projection matrix就变成了3x3的matrix，也就是homography。

当知道两个相机的姿态，可以用三角定位来确定一对对应特征点的3D坐标。如果已知3D点和图像中的投影点，也能算出相机姿态，这个问题叫做camera resectioning。

在已知相机矩阵的情况下，图像点的坐标根据相机矩阵K进行normalize之后，它们之间的关系跟essential matrix有关，这里用E矩阵来表示这是已知K的情况下的F。从E中可以计算出四个可能的相机姿态解，不过只有一个能让所有点都在两个相机前面。E和H的区别是，H假设了看到的点在同一个平面，所以可以把一个3D点定位到一个2D点。E没有平面假设，只能把一个3D点定位到另外一个图像的一条线上。E和F的区别是，E描述了同一个3D点在左右两个相机中的3D坐标的关系，而F描述了同一个2D点在左右两个相机中坐标的关系。

为了得到robust的解，还可以用ransac。在多帧的计算中相机姿态的误差会累积，这时用bundle adjustment优化3D点和相机姿态。

POSIT
这本书中提到了POSIT算法，用来计算已知物体大小的R，t运动。我们需要知道物体上4个不共面的点。算法首先假设这些点都在同一个深度，它们的大小变化仅仅跟相机距离物体远近有关。也就是说假设物体距离相机足够远，我们可以忽略物体的深度变化，所以物体上的点深度都一样。这个假设也叫weak perspective approximation.

从已知的点可以计算出一个并不是很准的pose，通过这个pose又可以反投影到4个2D点，然后根据它们和3D点的对应关系又可以更新pose，一直到pose收敛。

注意这里假设物体距离相机很远，所以物体上面点的深度变化可以忽略。如果这个假设不成立，那么pose要么是错误的，要么不会收敛。更多的共面的点也不会让算法更准，反而会导致错误的结果。更多的不共面的点则可以帮助减少误差。这个不是很理解，既然本来选取的点就不共面，表示深度不同，可是算法本身还假设深度相同，是不是有点矛盾？

在旧版的opencv中，cvPOSIT只能读取一个focal_length，因为这里假定像素的x和y方向是正方形。

Optical flow and velocity estimation

According to this, structure from motion solves two problems: correspondence for 2D motion in the image, and reconstruction for 3D motion of the camera.

Correspondence is often solved by optical flow. Let the pixel intensity be E(x,y,t), and suppose the brightness pattern is displaced by dx, dy over time dt, then the intensity of the displaced pixel should be the same as the original one: $E(x,y,t) = E(x+dx,y+dy,t+dt)$. In other words, the total derivative of E w.r.t time is zero: $\frac{\delta E}{\delta x}\frac{dx}{dt}+\frac{\delta E}{\delta y}\frac{dy}{dt}+\frac{\delta E}{\delta t} = 0$.

If we denote $E_x = \frac{\delta E}{\delta x}, E_y = \frac{\delta E}{\delta y}, E_t = \frac{\delta E}{\delta t}, v_x = \frac{dx}{dt}, v_y = \frac{dy}{dt}$, then the equation becomes $E_x v_x + E_y v_y + E_t = 0$, which is known as the brightness constancy equation (BCE). $E_x, E_y, E_t$ are measurable, while $v_x, v_y$ are the unknown flows. One BCE is insufficient to solve the flows. Therefore, to solve it we have to consider a small window of adjacent pixels. For instance, LK algorithm assumes the motion field at a given time is constant over a block of pixels. For the block of n pixels, there are n BCEs. This linear over-determined equation could be solved by least square estimation.

Once we have the flows, we can estimate the 3D motion. Homography describes the linear position relationship between feature points on two different planes. Suppose the camera takes images of the ground during flight, the visual features in two consecutive frames are related by a 3x3 matrix H, assuming the ground plane is flat. If R and T are the inter-frame rotation and translation, N is the unit normal vector of the ground plane in the camera frame, d is the altitude, then $H = R + \frac{1}{d}TN^T$, and thus $T=d(H-R)N$.

Based on this, when UAV is moving slowly, the rotation is negligible. Thus we can assume R is an identity matrix. As T is estimated, the velocity vector v in UAV body frame can be computed by $v = \frac{T}{\Delta t}$.

A simple linear KF could be used to estimate the UAV position. The measurement is the estimated velocity based on the homography, the linear states $x_k$ include the position and velocity of the UAV. The state x is updated using the prediction model: $x_k = F_k x_{k-1} + B_k u_k + w_k$. Essentially, it means $x_t = x_{t-1} + \dot{x_{t-1}} \delta t + \frac{1}{2}a \delta t^2 + N(0, Q_k)$ for position, and $\dot{x_t} = \dot{x_{t-1}} + a \delta t + N(0, Q_k)$. $u_k$ is the system input, i.e. the UAV acceleration. We assume the acceleration follows a zero mean normal distribution. $w_k$ is the process noise, which follows $N(0, Q_k)$.

The measurement model is $z_k = G_k x_k + v_k$, where $v_k$ is the measurement noise following $N(0, R_k)$.

OpenCV for secret agents - Motion amplifying camera

在007的电影中，Bond经常需要查看被隐藏的武器。通常他使用的x ray，红外线等仪器，但是这些仪器也很容易被其他间谍探测到。其实仅仅使用相机分析人的移动就能得到很多信息，比如某个人是不是在看一个方向，或者一条腿一直在动等等的肢体语言分析。我们可以把某种运动不断重复实现放大，就好比水面的波纹不断的扩散，这种方法叫做Eulerian video magnification.

Eulerian video magnification是基于Eulerian specification of the flow field。假设有一条河，Eulerian specificaiton描述了某个位置在某个时间的水流速度。这个速度在高山的泉水会快，在冬季的河口会慢，在河面会快，在河底会慢。我们可以用它来描述在某个位置，某个时间的物体运动。我们可以把不同时间和地点的运动叠加起来，达到强化运动的效果。

另外一种表达方式是Lagrangian specification,描述了某个物体在某段时间的位置，比如河里的一粒沙子肯呢过需要几年时间从山顶流到河口。它好比许多计算机视觉的程序，描述的是一个物体或者特征在一段时间内的移动。

FFT
我们通常用一段波形图来表示声音信号，波峰代表大声，波谷代表小声。在一段视频中，每一个像素也可以被看做是一个有起有落的波形。假设我们同时用相机和麦克风来记录一个节拍器，那么它发声的波形和指针在图像中运动的波形相一致。所以无论是声音还是图像都能用频率来描述。我们通过把图像转换到频域，选取特定的频率，再转换回来，保留想要看到的运动模式。

在原始的图像中运行FFT会很慢，而且这些频率对应在每个像素的运动，会有很多噪声，而且细节过多。因此我们把图像downsample，不过我们也希望保留对运动很重要的边缘。

可以用Gaussian filter进行downsampling，每个像素都是周围像素的加权平均，然后每隔一个像素去掉一个像素，这样每一帧的大小都是上一个图像的一半，就得到了Gaussian image pyramid。

为了保留边缘，我们用Laplacian image pyramid。在已经得到的Gaussian image pyramid中，我们选取第i+1层图像，通过复制像素值把它的大小扩大一倍，再使用Gaussian filter。我们把得到的图像和在Gaussian image pyramid第i层的图像相减，就得到了Laplacian image pyramid的第i层图像。所以Laplacian image pyramid中的图像就是一个模糊的，downsampled的图像和另外一个更加模糊的，经过两次downsample，一次upsample的图像的差值。

为啥这样就得到边缘了呢？边缘实际上是局部对比很大的特征，非边缘就是局部平滑的区域。如果我们把一个平滑区域变得模糊，它还是平滑的，所以和原来区域的差值为0.反之差值不为0，这样就能找到边缘。

我们不仅downsample FFT的输入，也upsample IFFT的输出，这样就可以得到和原始图像大小一样的图像。

Convert for_each to for

In c++11, you can use for_each as std::for_each(fts.begin(), fts.end(), [&](Feature* i){do something});, which is really convenient. However, this requires using -std=c++11 in cmake and it somehow conflicts with SSBA.

In order to convert for_each to for loop and avoiding to use -std=c++11, there are several things to do. Take the setExistingFeatures defined here for example,  we have to change const Features& fts to Features& fts first, otherwise an error of "conversion from const requested" will appear.

Next, for fts.begin(), fts.end(), we have to define an iterator, std::list<Feature*>::iterator it = fts.begin(); it != fts.end(); it++, which could be used in the for loop.

Finally note that it is a pointer to a structure, to access the members in the structure, we have to use (*it)->px[1].

OpenCV for secret agents - Rearview camera

这一章讲的是Bond的座驾如何自动检测到后面的追踪者。为了检测车辆后视镜里面的车头灯，可以假定它们都是白色的圆形，然后用blob detection，分为五步
1. 用二值化处理，把高于某个阈值的亮度设置为白色，反之为黑色。
2. 找到每个blob的轮廓。
3. 把相邻的blob融合在一起。
4. 计算blob的特征，比如中心点，半径等。
5. 去掉那些不符合条件的blob。

为了区分不同颜色的车灯，还需要转换到HSV颜色空间。
Hue指的是颜色在颜色轮上面的角度，红色是0， 绿色是120，蓝色是240。
Saturation指的是颜色与灰度值之间的距离，比如rgb的最大值减去最小值。
在Opencv中，为了能用一个byte存储hue的数值，hue被压缩到了0到180之间。想要更精确的数值，就要用0到360之间的浮点数。

在测量距离的时候，可以用 物体在图像中的大小/焦距 = 物体实际大小/距离。左边的单位可以是像素，右边是米。有几种方法可以测量距离
1. time of flight相机。这种相机发射一束光到物体上，然后测量反射光的强度。一些相机，比如Kinect，使用红外线光。但是这种相机会受到其他强烈光源的干扰，所以不适合检测车灯。
2. 双目相机由两个相机组成，它们之间的距离是已知的。通过图像每个点的disparity，就是像素距离，可以得到实际距离。不过通常计算量比较大。
3. Structure from motion, 只需要一个相机，不过需要知道它移动的距离。从不同地方的相机采集的图像中可以像双目相机那样算出距离。这里需要假设物体是静止的。因为007的座驾和后面的车灯都在移动，这种方法也不行。

一步步学习SFM 三

之前写的VO在feature很丰富的时候，比如fountain系列，貌似可以使用了。但是在面对草地等特征不足的时候，或者帧数增加的时候，solvePnPRansac就会找不到足够的inlier。在这篇博客中，作者提到了关键帧提取的重要性。并不是每一帧都要加入地图中，而是选取距离较远而且匹配成功，运动估计也正确的关键帧加入到地图中。

在code中，关键帧的定义是vector< FRAME > keyframes;进行匹配后要判断NOT_MATCHED，TOO_FAR_AWAY， TOO_CLOSE。这里注意每一个新的图像都是跟上一个keyframe匹配，而不是跟上一个图像匹配。

为了检查为什么inlier不够，我们可以把反投影得到的点显示出来。
cv::line(reprojected,imgPoints[ppt],projected3D[ppt],cv::Scalar(0,0,255),1);表示在名叫reprojected的图中用红色的直线连接原始的点和反投影点。
cv::line(reprojected,imgPoints[inliers[ppt]],projected3D[inliers[ppt]],cv::Scalar(0,0,255),1);在图中显示inlier，也用红色的直线连接。
for(int ppt=0;ppt<imgPoints.size();ppt++) {
cv::circle(reprojected, imgPoints[ppt], 2, cv::Scalar(255,0,0), CV_FILLED);
cv::circle(reprojected, projected3D[ppt], 2, cv::Scalar(0,255,0), CV_FILLED);
}
用蓝色点表示原始点，用绿色点表示反投影点。
cv::circle(reprojected, imgPoints[inliers[ppt]], 2, cv::Scalar(255,255,0), CV_FILLED);用蓝色加上绿色表示inlier点。

在inlier非常少的时候，光流的匹配貌似没有问题，可能是Find2D3DCorrespondences出现了问题。不过即使在inlier非常少的时候，found 1187 3d-2d point correspondences, 说明对应点的数目并不少，不知道为什么solvePnPRansac无法计算R，t。

Find2D3DCorrespondences在之前的点云中寻找当前图像中也出现的匹配点，貌似没什么问题。可能是计算3D点的时候误差逐渐增大，导致一段时间之后2D和3D的对应虽然可以找到，但是计算出的运动完全错误。这个问题在点云中也可以看出来，多个图像之后点云更加分散，导致3D和2D匹配计算运动很不准。在TriangulatePointsBetweenViews中减小反投影点残差的阈值，可以得到更准的3D点云，得到的inlier也就更多。

无论误差大小，总是需要处理从新初始化的情况，所以要拼接点云。在Find2D3DCorrespondences之后是FindPoseEstimation得到R，t，然后TriangulatePointsBetweenViews。 这时候就要用到之前求得的相机姿态。

这里又发现一个问题，PruneMatchesBasedOnF和FindCameraMatrices都是在用GetFundamentalMat，只不过PruneMatchesBasedOnF多了一行matches_matrix[std::make_pair(working_view,older_view)] = FlipMatches(matches_matrix[std::make_pair(older_view,working_view)]);原始代码中两个函数都要运行。也许是8点算法需要先除掉outlier，然后用inlier再计算一遍F才能准。

因为暂时早不到问题的根源，所以先用两个图像匹配，利用kitti中提供的groundtruth作为尺度。奇怪的是运行图像0到7的时候，提示三角定位失败，但是单独运行图像6和7则是成功的。发现是TriangulatePoints中的P必须是identity matrix，不能是上一次相机的姿态。可能是因为上次的姿态计算有误差，造成三角定位的误差过大而出错。

除了运行的问题，它的速度也偏慢，只有2Hz.可以尝试使用更快的特征点检测，比如SVO中用的fast，具体安装参考这里。

8算法不能处理所有点都在同一个平面的问题，具体见这里和这里。为了更好的计算E，可以使用5点算法。算法的code可以在这里，和这里找到。

OpenCV for secret agents - head gesture recogntion

本章主要讲解如何判断一个人在点头还是在摇头。人脸识别用的是opencv的cascadeclassifier，在识别成功后用goodFeaturesToTrack检测人脸的特征，然后用calcOpticalFlowPyrLK来追踪这些特征。如果特征点的中心上下移动，就认为是点头。如果是左右移动，就认为是摇头。

在跟踪特征的时候要用到光流，这里有三个附加说明：
1. 我们不区分相机和人脸的运动
2. 特征的颜色和亮度在图像中保持相似
3.相邻的特征有相似的运动

在opencv中，calcOpticalFlowPyrLK函数用了Lucas Kanade方法计算光流。这个方法基于每个特征点周围的$3\times 3$的图像块，然后在相邻图像中寻找能使得残差平方最小的匹配图像块。opencv中还用了图像金字塔来进行多尺度处理，这样就能处理大的或者小的运动。其他的函数，比如calcOpticalFlowSF或者calcOpticalFlowFarneback都是跟踪每一个点，所以calcOpticalFlowPyrLK的计算量更小，处理不同远近的人脸也更加稳定。

goodFeaturesToTrack选取了更容易被跟踪的点，抛弃了不易被跟踪的点，比如反射的阳光，树枝的交叉点，因为这些点会很快变化或者消失。相机的视角变换可以用warping来模拟，这样不同视角下都稳定出现的点就会被选取。good features to track是基于minimum eigenvalue corners和Harris corners的改进。更先进的特征点检测，比如FAST,ORB,SIFT,SURF,FREAK更广泛的选取特征点，计算量也更大，不适合用在基础的光流计算上。尤其是对于头部运动的识别来说，速度更快更重要，并不需要找到很多的特征点。

SVO论文笔记

SVO提出了一种基于向下看的相机和IMU的定位算法。论文开始先总结了运动估计的方法，主要有两种。

第一种是基于特征点，现在图像中选取角点等特征，然后在相邻图像中匹配，用epipolar集合来回复相机运动和场景。最后最小化反投影残差来优化相机姿态和场景。这种方法的成功在于有很多特征点检测和匹配的算法，甚至可以用在两个图像之间运动很大的情况。缺点是需要设定检测和匹配的阈值来剔除错误的匹配，而且很多检测方法往往不精确，导致运动的漂移需要平均很多特征点才能减小。

第二种是直接的方法，基于图像中的像素值。这里使用局部的梯度，包括大小和方向。当图像中特征点很少的时候，或者图像有模糊的时候，这种方法都好于特征点法。计算photometric error需要比反投影残差更多的计算量，不过不需要特征点的检测和匹配。

之前多数单目视觉里程计都是基于PTAM的，它是基于特征点检测的SLAM算法，通过跟踪和匹配上百个特征点实现。它通过并行计算运动估计和建图，使用高效的关键帧的BA，来实现实时性能。不过PTAM主要用在室内桌面的AR，如果在室外使用需要限制关键帧的个数。

直接的方法有DTAM，用最小化一个能量方程来计算每个关键帧里面的深度值。相机的姿态通过匹配整个深度图来计算。这种方法需要很大计算量，所以只能用GPU。

对比之前的方法，SVO主要的贡献在
1. semi-direct方法，比之前的方法更准确，快速。
2. 基于概率的构图方法，可以处理outlier。

SVO使用了两个并行的thread，一个用来估计相机姿态，另一个构建地图。

估计相机姿态时，第一步是最小化相邻两个图像中相同3D点投影的photometric error。反投影的点对应的2D点通过匹配图像块进行优化。最后同时优化姿态和反投影残差。

在论文的motion estimation部分，作者假设像素的残差成正态分布，variance是1.与之前方法不同，并不是很多的点都有深度，而是只有稀疏的特征点有深度。在每个特征点周围选取4x4的图像块，我们要找到能使得这些图像块残差最小的相机姿态。

为了减小漂移，相机的姿态应该和地图对应，而不是前一帧。所有能在当前相机中看到的已知3D点会被反投影到图像中，对每个反投影点，都找到它在关键帧中对应的图像块，然后在跟当前图像中的图像块对比。

在姿态和结构优化部分，作者对运动和3D点分别使用BA来优化，然后在将两者放在一起优化。跟只是两帧之间对比的sparse image alignment比较，加入当前图像和关键帧以及地图的对比能得到更准确的结果。

在地图构建中，我们根据当前图像和相机的姿态来估计每个特征点的深度。构建地图的时候，一个基于概率的深度滤波器会对每个2D特征点初始化，来寻找对应3D点。开始的时候每个深度的不确定性都非常大，之后每个图像中都根据贝叶斯定理优化深度。当一个深度的不确定性足够小的时候，一个新的3D点就被加入地图，用来做运动估计。

这部分可以参考这篇论文，大概是讲如何从多个图像中估计深度。在图像I中，在光轴上一点x(Z),距离相机深度为Z，它在I中的图像块w对应另外一个图像I'中的图像块w'，可以用NCC来计算w和w'的相似度。通过观察作者发现用寻找NCC最大值的方法计算Z，要么得到的深度很准，要么就随机分布在Zmin和Zmax的区间内，也就是可以用一个gaussian+uniform的概率分布来描述。给定一个初始的先验概率，接下来就可以用bayesian inference来计算最大化后验概率的深度。

在SVO的论文里，depth filter的大意貌似是这样的。计算了某个点u在图像Ir的深度rP之后，在图像Ik中可以找到u的对应点u',如果把u'移动一个像素，就能得到一个新的u对应的3D点rP+，对深度估计的误差就是rP和rP+之间的距离。为什么rP的variance是把u'移动一个像素之后得到的呢？具体要参考这里。更多关于为何使用depth filter参考这里。

仔细看mapping部分，每个depth filter都对应一个关键帧。初始化的时候每个点的不确定性很大，初始值就是关键帧中深度的平均值。接下来的每个图像中，我们在epipolar line上面寻找对应的图像块，然后通过三角定位计算深度。跟这篇论文中不同的是，为了应对很大的深度变化，SVO使用了inverse depth。

算法实现
在最开始的两帧，SVO使用了平面假设来估计一个homography，然后用三角定位初始化两帧里面点的深度，这个过程和PTAM相似。为了应对大幅度的运动，在sparse image alignment用了coarse to fine方法。

如果当前帧距离所有关键帧的距离超过场景平均深度的12%，那么当前帧就被选为关键帧。为了加快效率，SVO中的关键帧数目是一定的，所以每加入一个关键帧，都会把最老的一个关键帧去掉。

在mapping thread中，图像被分成了30x30的小格子。每个Shi-Tomasi score最高的FAST角点会被加入depth filter，除非那个格子里面已经有了2D和3D对应的特征点存在。这样就可以得到平均分布的特征点。

推荐另外一篇非常好的SVO论文博客。

运行SVO
从github上面下载并安装好svo之后，可以运行test pipeline来看结果。在catkin_ws里面catkin_make, 生成的.exe文件在catkin_ws/devel/lib/svo里面。作者给的airground dataset的pose可以用这里提到的方法存在txt文件里面。

Visual odometry - OpenMVO

I have found several great sources on VO, namely this, this, and this. Since I would like to work on monocular VO, I use this first. In this blog, I will write about its implementation.

The original code is written for windows, and I want to port it to Ubantu in ROS catkin workspace. So I do not follow the file structure but use the one for catkin. Whenever a third party library is needed, I include it in the cmake.

At first, we have to detect features using FAST. We need to define a class called frame to process the images. Several third party libraries are needed, similar to SVO. To use Eigen, I copy the CMakeModules folder in SVO to my src folder, which contains FindEigen.cmake. Regarding Sophus, I encounter an error saying that Sophus.cmake cannot be found. This is wired because in SVO it finds the library without any problem. After debugging, it turns out that I should use FIND_PACKAGE(Sophus REQUIRED) in cmake instead of FIND_PACKAGE(sophus REQUIRED). The name should be exactly the same and the first letter should be CAPITAL.

For the constructor in the frame class, : key_pts_(5) means to set key_pts_ to 5, as mentioned here.  In Frame.cpp, it turns out that we could not use #include "feature.h", which leads to re-definition of frame class.

We also have to add

IF(CMAKE_COMPILER_IS_GNUCC)
SET(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++0x")
ELSE()
SET(CMAKE_CXX_FLAGS "${CMAKE_CXX_FLAGS} -std=c++11")
ENDIF()

as in SVO cmake to be able to use lambda expression, eg. 

std::for_each(key_pts_.begin(), key_pts_.end(), [&](Feature* ftr){ ftr = NULL; });

Since I am using Ubantu, I could not find _aligned_malloc, which seems to be only available in windows VS. So I delete the SSE2 related part in image_utils.h. 

Another issue often encountered is the re-declaration problem. For instance, in the point3d.h, we need to add
#ifndef POINT3D_H_
#define POINT3D_H_
and #endif
to avoid this.

In frame.h, when it says Vector3d does not name a type, we have to include abstract_camera.h, and  using namespace Eigen; solves this problem.

When I run the initial_position, it gives core dumped error, and it seems c2f is not executed. It also turns out that px_ref_it->x - px_cur_it->x, px_ref_it->y - px_cur_it->y are all 0. This is because I use two identical images for the frame 1 and 2. But even if I use different images, it still gives me segmentation fault. The reason is that I forget to initialize cam_(cam) in frame.cpp

Take note that vector is in namespace std, not cv.

Next problem is that scale is nan. The implementation seems to be problematic, and I probably should implement my own VO step by step.

In the FAST keypoint detection, the image is divided into several cells, and only one keypoint in every cell with the highest shi-tomasi score is selected, as shown in the following code
if (score > corners.at(k).score)
corners.at(k) = Corner(xy.x*scale, xy.y*scale, score, L, 0.0f);
There is an angle in the Corner defined in feature.h, which should hold the gradient information of the keypoint, but it does not seem to be in the code.  

OpenCV for secret agents - cat recogntion

The cat recognition chapter in the book reminds me of the recent 007 movie, Specter. The interesting things to note in this chapter is that the training cat images have to be rotated to upright position. The function getRotationMatrix2D is used to define the rotation and warpAffine is used to rotate the image. Obviously some black regions will be introduced in the image, and thus we can fill them by a specific color. The author uses 50% gray, as it does not tend to introduce bias into the image histogram equalization.

Haar cascades and LBPH

Opencv for secret agents是一本非常棒的opencv指导用书。有一章讲的是machine learning。在一张图像中我们可以看到有特点的形状或者模式，而这些模式往往只在特定尺度下出现。为了生成Haar cascade，图像的不同区域会经历尺度变化，这样我们就能每次只关注一些像素。像这样对图像取样叫做window。我们可以用window中的一些区域的像素减去另外一些区域的像素值来判断是否包含一个灰暗的部分和一个明亮的部分，从而可以对比当前window和一些常见形状，比如边缘和角点。如果一个window和某个特定形状很相似，我们就可以选择它作为一个feature。对于同一物体，通常我们能够在相似的地方和尺度找到相似的feature。
并非所有的feature都同样显著。如果一个feature在物体中很常见，我们就把它放到positive training set里面。反之，不常见的就放到negative training set里面。根据feature描述物体的程度，我们可以赋给它们不同的stage.多个stage就组成一个cascade。为了判断待检测目标是不是已知样本，每个stage都必须通过。

一步步学习SFM 二

上一篇看了理论，这里主要看code。

在读取所有图像后， 用MultiCameraPnP初始化。如果没有给相机矩阵，在MultiCameraDistance里面会自动初始化一个。

OnlyMatchFeatures会用OFFeatureMatcher把所有已经读取的图像之间的光流计算出来并进行匹配，然后把结果存储在matches_matrix里面。

然后PruneMatchesBasedOnF会计算F，然后把不符合的匹配去掉。GetBaseLineTriangulation可以在所有图像中找到两张homography匹配最好的，然后计算R，t。

AdjustCurrentBundle使用SBA把点云和相机轨迹进行优化。其中有个参数是K = Count2DMeasurements(pointcloud);就是同一个点在几个图像中都被观察到了。如果没有检查新得到的点是否在已经有的点云中，不知道还能不能使用BA。

如果只计算当前frame与上一张之间的光流，在计算F的时候使用的也是这两个frame的匹配。FindCameraMatrices会输出tmp_pcloud表示outCloud。

这里遇到一个问题，就是TriangulatePointsBetweenViews总是找不到原来点云中的匹配点，导致所有的点都被认为是新的。在onlymatchfeature中，每一张新的frame都要跟原来所有的frame做匹配，否则TriangulatePointsBetweenViews找不到对应点。TriangulatePointsBetweenViews是以older view和working view为基准，所以不能只让当前frame和前一frame进行匹配。

还有一个问题是GetRGBForPointCloud总是报错，BUG: point id:1235490744 should not exist for img #2 which has only 9280，函数是在AdjustCurrentBundle中调用的GetRGBForPointCloud(pointcloud_beforeBA,pointCloudRGB_beforeBA);

可能是int pt_idx = _pcloud[i].imgpt_for_img[good_view]超过边界的问题。经过检查，_pcloud[i].imgpt_for_img.size()是2,表示imgpt_for_img里面只有working view和older view的匹配。后来发现PruneMatchesBasedOnF只处理了当前frame和前一个frame，加入for之后_pcloud[i].imgpt_for_img.size()就是3了。但是那个BUG还是会出现。

经过长时间debug，终于发现是TriangulatePointsBetweenViews函数中初始化new_triangulated[j].imgpt_for_img = std::vector<int>(2,-1);的问题，imgpt_for_img的size可能比实际用到的小。

should be pcloud[pt3d].imgpt_for_img[1] == submatches[ii].queryIdx instead of pcloud[pt3d].imgpt_for_img[0] == submatches[ii].queryIdx

在使用code的时候，如果是fountain dataset效果还可以，换成其他图像可能会计算不出有效F,需要把FindCameraMatrices函数中if(fabsf(determinant(E)) > 1e-07)阈值调高。

在连续运行的时候，会出现not enough inliers to consider a good pose，是因为在solvePnPRansac中inlier不够。根据这里的分析，可能是没有关键帧的提取。之后我会分析如何改进。

Multiple definition problem

I often see multiple definition problem when including the same header file in several places. For instance, if I have a common.h, and put all the function body plus declaration in it, then there is a problem.

It turns out that I have to put function declaration in the common.h, and put the body in common.cpp, which addresses this problem.

一步步学习SFM

有本很好的学习OpenCV的教材，mastering opencv with practical computer vision projects, 在第四章讲解了SFM。SFM解决的是从运动相机拍摄的图片中还原运动轨迹和场景几何结构的问题。

从图像中计算相机运动

先从已知条件开始，我们知道两张图片，由相机在同一场景中运动得到。书中用的图片在这里。要恢复相机运动，我们要用到fundamental matrix F和essential matrix E。F可以从findFundamentalMat函数中得到。为了得到E，我们需要先校准相机，得到相机矩阵K。然后E=K.t*F*K.E是个3x3的矩阵，描述了同一点x在两个图像中的关系,x'Ex=0.

用特征描述算子匹配特征点

为了得到同一点在两张图像中的位置x和x'，我们需要找到匹配的点。我们可以用SURF来寻找特征点和描述算子，然后用brute force来寻找匹配。不过这些匹配中很多是错误的，所以需要过滤掉这些错误的匹配。opencv的brute force方法已经有了cross check filtering，只有当一个特征点对无论从图像A到图像B还是图像B到图像A都是最佳匹配的时候，它才会被保留。除此之外，在计算fundamental matrix的时候，我们只保留inlier。

用光流匹配特征点

光流可以用calcOpticalFlowPyrLK函数得到。从图像A的特征点计算光流到图像B的到的新特征点，并不一定会和图像B中检测到的特征点完全匹配。我们需要用KNN来把它们匹配在一起。另一个在SFM中常用的减小误差的方法是ratio test，它处理图像A中某特征点匹配到图像B中两个点的情况，这时我们不知道两个点哪个才是真正的匹配。ratio test会去掉图像B中两个相距很近的特征点，因为这时两个点都有可能是匹配点，我们完全无法得知该选择哪一个。判断方式是两个匹配点距离图像A中特征点距离的比值不能太大。

处理完距离太近的点，我们还要处理重复的点。这里使用了STL里面的set函数，可以给元素排序。关于set的find的说明在这里。注意原来书中用的是指针vector<DMatch>* matches，在自己写的函数中需要替换成std::vector<cv::DMatch>。我理解的处理重复的点是这样的。因为现在是把跟踪的点和图像B中实际的点做匹配，同一个跟踪点可能被匹配多次，这时候就通过if (found_in_cur_points.find(_m.trainIdx) == found_in_cur_points.end())来判断是不是之前出现过这个跟踪点。如果是新的跟踪点，我们还要使用原来图像A中的特征点的id，而不是图像A中跟踪成功的特征点的id。

使用光流的好处是比较快，能产生更多特征点，得到dense reconstruction。光流通常只用很基本的特征，比如特征点周围的patch，SURF则会考虑更多高级的特征。

恢复相机运动轨迹

相机运动可以用矩阵P表示，包含旋转R和平移t。一个很重要的关系是x=PX，x是图像中的2D点，X是空间中的3D点。这个公式描述了图像点和空间点之间的关系。我们对E进行SVD，然后乘以矩阵W。SVD把E分解为了旋转和平移两个部分。我们现在只得到了一个运动矩阵，它是相对于第一个相机而言的。我们假定第一个相机没有旋转和平移。所以通过x=PX恢复的3D点的坐标原点就是第一个相机。

很多时候F矩阵是错误的，从而运动矩阵也是错误的。为了判断运动的正确性，我们可以检查旋转矩阵，因为它的determinant必须是1或者-1.

重建场景

从2D特征点匹配和运动矩阵，我们已经得到了x=PX, x'=PX'。x和x'是图像A和图像B中的匹配点，X是空间中的3D点。用所有的特征点，我们可以得到一组公式来求解X。假定X=(x,y,z,1)t，可得AX=B。从而可以得到2D匹配点对所对应的3D点，这个过程叫做三角定位。这里注意2D点也是在homogeneous coordinates下，所以在x,y后面加个1.同时这些坐标需要normalized，就是说在使用之前要先乘以相机矩阵K。

因为只有一个相机，那么问题来了，恢复出来的几何结构单位到底是mm还是m呢？这个我们无从知晓，所以恢复的结构是up to scale的。两个相机之间的运动向量的单位可以是mm也可以是m，它只是一个unit scale。我们只能说两个相机之间的距离是一个单位长度，而不知道真实的物理距离。当有多个运动的时候，每两个相机运动的单位长度都是不同的，它们之间并不存在一个统一的单位。

为了得到更准确的重建，我们可以从得到的3D点反投影到图像中得到2D点，然后比较这些新的点和原来图像中的特征点的距离。如果距离很大，那么我们的三角定位得到的3D点很可能是错误的，我们就需要去掉这个点。这些距离的平均值可以用来作为一个全局的评判，如果平均值过大，那么P矩阵是错误的，可能因为错误的E矩阵或者错误的特征点匹配导致。

从多幅图像中重建场景

因为不同的图相对给出的重建有着不同的尺度，多幅图像重建并不是重复两幅图像重建过程那么简单。我们可以用PNP来根据已知空间点来求得新的相机位置。另一种方法是三角定位更多点然后观察它们是不是符合已经重建的场景，这时我们可以用ICP来求得相机位置。这里我们使用opencv中的solvePnP函数来实现第一种方法。

我们首先要找到一个baseline来确定场景的尺度。这个可以通过第一幅和第二幅图像得到相机运动矩阵，然后再三角定位获得空间点的位置。对每个空间的3D点，我们还需要记录它原来的2D点的位置，然后可以在新的图像中匹配得到对应点。这样我们就能获取新的相机位置。注意这里我们用solvePnPRansac而不是solvePnP，因为前者能更好的应对outliers.获得新相机位置之后，我们可以继续三角定位新的3D点。

我们需要新建一个结构来记录3D点和对应的2D点
struct CloudPoint {
cv::Point3d pt;
std::vector<int> index_of_2d_origin;
};
index_of_2d_origin 记录了3D点在图像中所有特征点的index.


重建优化

SFM中一个很重要的过程就是优化重建的场景，又叫做BA。我们把所有已知的数据合并成一个整体。这些数据包括空间点的位置和相机的位置。优化的判断依据是3D点反投影到图像得到2D点之后与原来真实的2D点之间的残差。

我们用SSBA来实现优化过程，具体由CommonInternalsMetricBundleOptimizer函数用来实现优化。这个函数需要知道相机参数，3D点云，每个3D点对应的2D点，和每个相机的位置。

用PCL实现3D点云可视化

首先把3D点转变为PCL的数据结构，也可以把RGB信息包括进去，然后用SOR来过滤outlier。

总结

这个SFM只是最基本的算法，有很多可以改进的地方。比如使用更加精确的三角定位方法，例如N view三角定位。对于SFM，还有很多其他的资源，如libMV，Bundler, VisualSfM。如果需要实时的进行场景重建，我们就要用到SLAM。

code的结构

在这里有上面的code。
在main函数中，第一步是RecoverDepthFromImages.
OnlyMatchFeatures我们首先用光流或者特征点匹配来匹配相邻图像的特征点。
PruneMatchesBasedOnF算出F矩阵之后去掉不符合的特征点
GetBaseLineTriangulation在两个图像中找到初始点云。用homography找到inlier最小的两个图像进行初始化，用的函数是FindCameraMatrices。先找到F矩阵，在计算出E矩阵，从E中回复R和T，判断四个解答中哪一个是对的。如果F矩阵的inlier足够多，那么认为它是合适的。接下来是TriangulatePointsBetweenViews，先得到两张图像中的对应点，再三角定位匹配点。然后我们去掉那些反投影残差很高的点。我们还要判断哪些点已经在之前的点云中出现过，避免重复添加相同的点。

得到初始的匹配之后，我们以此运动为基准处理以后的图像。用Find2D3DCorrespondences找到新的图像中特征点在已有点云中的对应特征点, 然后用FindPoseEstimation找到新的相机的运动轨迹。根据已知2D-3D点计算运动用的是solvePnPRansac。

得到几个相机的运动轨迹和点云后，我们可以用ssba来优化。关于ssba的解释在这里。要build这个library，新建一个3rdparty文件夹，然后在里面放入ssba的source code。根据这里提供的方法，再新建一个build文件夹，就可以进行build。在cmake，make之后，build里面会生成两个.a文件，就是static library。要在cmake里面link这个library，一个简单粗暴的方式就是直接把.a的full path，包括.a文件名，写到cmake的target_link_libraries.另外还要在include_directories中加入3rdparty/SSBA-3.0/，这样才能找到那些header file。

solvePnP

I have used solvePnP a lot recently for camera pose estimation. Here is a fascinating post about some possible issues of the function.

Loopy BP, MRF

今天读到一篇介绍BP和MRF的blog, 在stereo vision中，如果只考虑单独的像素做匹配，而忽略像素周围的pattern，就容易导致不连贯的disparity map。实际上我们希望disparity map中相邻像素有相同的值。这个时候就可以用到MRF。MRF是无向图，但是跟Bayesian不同的是它可以有cycle和loop。

蓝色的点表示观测到的变量，就是像素值。粉色的点表示隐藏变量，就是disparity。通常隐藏变量叫做label。node之间的link表示dependency，比如中间粉色的点只跟周围四个点和上面的蓝色的点有关。这个某点只跟周围点有关的假设就是Markov假设。这个假设使我们能够高效的求解隐藏变量。

如果用MRF来表达stereo vision，它的energy function就是

Y表示观测变量，X表示隐藏变量。i是pixel的index，j是xi相邻的node。给定一个图像Y和一些label X，这个能量方程求得了每个link的cost的和。我们的目标是找到一个label X，比如disparity map，使得这个能量方程最小化。接下来我们分开来看data cost和smoothness cost。

Datacost主要指把label xi赋值给data yi造成的cost。对于正确的匹配，datacost很低。对错误的匹配datacost就很高。常用的衡量datacost的有差值绝对值的和，SSD等。

Smoothness cost确保相邻像素有相同的label。我们需要一个函数来惩罚相邻像素有不同label的情况。常用的函数有如下几种
Also known as the Potts model.Truncated linear model.Truncated quadratic model.

如何选取合适的函数和参数看起来就像黑魔法，大多数paper并没有提到应该怎样做。

Loopy Belief Propagation

因为图像中有很多像素，disparity value也有很多可能，所以很难找到MRF的精确解。LBP提供了一种方法来寻找近似解，类似的方法还有graph cut, ICM.不过LBP不保证convergence。

LBP是中用来传输信息的方法，当一个node收到了所有信息的时候，它就发给相邻node一个信息。下图展示了从x1传送到x2的过程。

x1首先需要从A,B,C,D接收到信息，然后才会给x2传输信息。x2不会返回给x1信息。准确来说信息的定义是，表示从node i发送label l的信息给node j。换言之就是node i对node j属于label l的belief。这些信息只在隐藏变量之间传递。一个完整的信息包含所有可能的label。比如node i会给node j发送如下信息

hey node j，我认为你是label 0，概率是s0

hey node j，我认为你是label 1，概率是s1

。。。

Node i记载了所有关于node j的可能性。概率的计算取决于MRF。

LBP的第一步是初始化信息。因为node要等到所有相邻node都发送信息，这就变成了一个鸡生蛋蛋生鸡的问题，因为所有node都会等待其他node发送信息，实际上谁也没有发送任何东西。为了解决这个问题，我们把所有信息都初始化成一个常数，通常是0或1.

LBP主体算法是iterative的。如同其他iterative的算法，我们可以在一定循环次数后结束，或者到energy的变化小于一个阈值。在每个iteration，信息在MRF中传递。信息传递的次序是随机的。一旦这个过程结束，我们就可以根据每个node的belief计算这个node的label。

接下来我们一个个来看信息更新，初始化，和belief的步骤，和三个不同算法sum product，max product, min sum。

用于信息更新的sum product

等式左边表示从node i发到node j，关于label l的信息。右边的y表示图像像素。这里我们遍历所有的label，在disparity map中共有15种。因为有加和，内积的计算，所以叫sum product。这个算法用于概率的计算，所以要用exp函数把data cost, smoothness cost，转换到在0到1之间的概率，这个概率越大越好。在中括号里面的是data cost, smoothness cost对于label l的所有信息的joint probability. 中括号外面的加和是对概率在变量l上的marginalization.

一个完整的信息是一个矢量

所以对于每个label都要遍历所有可能，复杂度就是O（L^2）.

连续对概率做乘积的时候，很快就会接近0.为了避免这个情况，我们要把信息向量normalize

进行初始化的时候，所有信息的概率都设为1.每个node的belief是所有信息的乘积。

这是node i对于label l的belief。为了找到最合适的label，需要遍历所有label然后找到最高的belief。

用于信息更新的max product
sum product可以找到每个node的最佳label。但是总体来说并不一定是最优解。举例来说，假设有两个变量x，y

P(x,y)	x=0	x=1
y=0	0.5	0.4	P(y=0) = 0.9
y=1	0.1	0.3	P(y=1) = 0.4
	P(x=0) = 0.6	P(x=1) = 0.7

表格外边的是变量的marginal。如果用单独的marginal计算，我们会选择x=1, y = 0,得到P(x=1,y=0) = 0.4。但是最佳的解是p(x=0,y=0) = 0.5。我们最关心的是Joint probability。此类问题经常会在maximum a posteriori (MAP)求解中出现，因为这时我们想找到全局的最优解。max product在sum product的基础上做了一点点改变

现在不再求和，而是计算marginal probability的最大值。

用来更新信息的min sum
和max sum相似，min sum也是计算每个node的max marginal，不过是在log space中。

这是个求解最小值的问题。在初始化的时候所有的数值都是0. 这时的belief是

不过因为我们其实在找最小值，称它为cost更合适。

在这些方法中，min sum是最方便实现的，它没有exp函数，只有加和。如果用sum product的话，就要在exp里面加上scaling来避免underflow。eg. exp(-DataCost(…)*scaling) * exp(-SmoothnessCost(..)*scaling), scaling是 0 到1之间的数.

ROS catkin init workspace error

I encounter an error while initializing a catkin workspace. We are supposed to mkdir src in the catkin_ws folder, and then catkin_init_workspace in the src folder. Then we step out in the catkin_ws folder again and catkin_make. 

Now the error occurs, setup.sh: rm: Argument list too long, this is probably because I have sourced the setup.bash. Use another terminal to catkin_make solves this problem.  

CPU和GPU

这篇blog讲解了GPU的入门知识。首先为何要用GPU，因为CPU的clock time已经几乎不能再增加，否则就要消耗更多power，需要更强大的降温处理。此外，一个高端CPU只有8个核，而一个普通GPU有96个核！CPU注重的是latency，就是完成一个任务需要的时间。GPU更注重throughput，就是单位时间内完成的工作量。

CUDA是NAVIDA构建的framework，可以在CPU或者GPU上面运行。在GPU上运行的程序又叫kernel，虽然看着很像serial program，但实际上是在多个GPU核上面运行的。通常一个CUDA程序包含一下几步：给GPU分配内存，将CPU上的数据传输到GPU上，在GPU上运行程序，将结果从GPU传回CPU。

视觉里程计

最近读到了一个很好的blog，讲的简单易懂。里程计就是车里面常见的记录里程的仪表，通过车轮转过的圈数统计汽车走过的距离。视觉里程计主要指机器人的6DOF的轨迹。

我们可以用单目或者双目相机来实现视觉里程计（VO）。双目相机的好处是可以得到准确的轨迹，比如x方向动了1米，而单目相机只能得到一个不能确定尺度的轨迹，比如x方向动了1个单位。不过如果机器人很小，双目相机的baseline就会很小，对于远处的物体，双目相机实际上相当于一个单目相机了。因为现在的无人机正在变得越来越小，所以Scaramuzza组主要在研究单目相机。

双目VO

对于双目相机，我们的输入是在t和t+1时刻的图像，输出是这两个时刻间机器人旋转和平移的矩阵。具体来说，我们先计算disparity map，然后用FAST算法检测特征点，用KLT进行匹配。为了使特征均匀分布，我们在每个grid中都选取20个特征点。

在计算disparity map之前，我们要先进行一些预处理。首先要做undistortion，用来处理相机lens的distortion。然后是rectification，使得epipolar line变得平行，这样disparity map就只需要在一个方向做block matching。

在disparity map里我们可以得到这些特征点的3D位置，这样就有了两个点云。接下来，我们需要得到这些点云在真实3D世界中的坐标。在匹配中选取哪些互相配对的匹配点，然后在这些inliers中计算运动矩阵。这里的inlier是通过maximum clique problem找到的，就是寻找一个graph中的subset，在这个subset里面所有node都是互相连通的。

我们可以用Levenberg Marquardt方法来求最小值，这里的目标函数就是特征点在t和t+1时刻图像的匹配度，还有它们的3D坐标在运动轨迹中的匹配度。

一个重要的hack是当一个很大的车占据图像的大部分的时候，scene rigidity的假设不再成立。这时我们只保留那些主要运动方向是向前的运动矩阵。这个hack会极大的提高算法在KITTI上的performance。

单目VO

和双目一样，单目VO的input也是两个时刻的图像，输出是R和T。只不过这里的T不考虑尺度。首先我们还是undistort这些图像，然后用FAST检测特征点。接下来用Nister的5点算法和RANSAC来计算essential matrix。在essential matrix中得到R和t。通过其他sensor得到尺度信息来更正R和T。

在OpenCV中，我们可以用FAST函数来检测特征点。然后用KeyPoint::convert来把KeyPoint类型转换成Point2f类型，用来做特征跟踪。KLT的函数是featureTracking。在KLT中，会有一些点被丢掉。当总特征点数很少时，我们需要重新检测特征点。通过匹配的特征点，可以得到essential matrix。因为essential matrix只有5个自由度，我们可以用5点算法来计算它。

如果特征匹配是完美的，我们只需要5个匹配就可以了。但实际上肯定有误匹配。所以需要RANSAC来筛选inlier。在每个iteration，我们随机选取5个匹配，然后计算essential matrix。接着查看其它点是否满足这个essential matrix，直到得到了足够多的支持点。在OpenCV中这一切都可以通过findEssentialMat实现。得到essential matrix之后，就可以计算pose。这个函数是recoverPose。相机的轨迹就是R_pose = RR_pose，T_pose = T_pose + TR_pose。

和双目VO一样，这里也假设几乎所有点都是rigid。但是我们可能会遇到一辆巴士驶过的情况。算法可能会错误的认为运动是朝向侧面的。所以如果T不是向前的运动，我们就忽略它。

Publishing images to http in ROS

If we want to view the image only, we could do it in a web browser. In ROS, there is a package named web_video_server as mentioned here, that achieves this. After the image is published, we have to rosrun web_video_server, and following the wiki, we only need to copy this in the browser: http://localhost:8080/stream_viewer?topic={ROS_TOPIC}.

For instance, if the topic is called /camera/image_color, then the address should be http://localhost:8080/stream_viewer?topic=camera/image_color, and we can see the image in the browser.

ubantu and point grey camera

We have to install flycapture drivers no matter we use win7 or ubantu. On win7, we only need to download the flycapture from the official website and it works out of the box. However, on ubantu we have to do several things.

The instructions I follow are basically taken from this. Note that in the README that came with FlyCapture ARM version, we have to copy all libraries to system folders. When it says do you want to restart udev daemon, type yes.

An error occurs

/usr/bin/ld: skipping incompatible /usr/lib/gcc/x86_64-linux-gnu/4.8/../../../../lib/libflycapture.so when searching for -lflycapture

It is not solved even after I restart the computer. I suspect that ARM version only works on embedded boards, not on desktop computers. So I follow the instructions here and it works.

In the code we have to include the header file by #include "FlyCapture2.h", but where is it? It turns out that we have to include /usr/include/flycapture in our cmake file.

Moreover, there is also a ROS package provided here. After installing it by sudo apt-get install ros-indigo-pointgrey-camera-driver, we only need to use roslaunch pointgrey_camera_driver camera.launch to use the camera.

Later I encounter another camera issue, as I could not get image from CM3-U3-31S4C-CS in Ubuntu 14.04.4 with ROS indigo and flycapture 2.9.3.43. No camera is detected in flycapture or rosrun pointgrey_camera_driver list_cameras. On the other hand, CM3-U3-31S4C-CS can be detected in Ubuntu 12.04 with ROS hydro for both flycapture and list_cameras command. However, there is no data output from the rostopics published by the camera, so I still could not get any image. Moreover, the camera works on my windows desktop with flycapture 2.8.3.1. 

Searching around, this post seems to be related, but I did not follow it. I uninstalled the flycapture and re-installed it. Previously, I did not see the prompt to enter user name, and this time I saw it. After installation was finished, the camera could work. 

Premier CS4 视频输出

编辑视频的时候经常遇到输出视频不流畅的情况。貌似是因为输出的帧率太高，文件太大导致的。尝试不同输出格式之后，发现H.264输出720p，帧率23的时候视频的流畅度比较高。

OpenCV for Secret Agents - image scene classifier

I found a great book about OpenCV application, called OpenCV for Secret Agents. Here are some interesting stuff from the book.

Python code for histogram intersection

def intersection (hist0, hist1):
  assert len(hist0) == len(hist1),
    'histogram lengths are mismatched'
 result = 0
 for i in range (len(hist0)):
   result += min(hist0[i], hist1[i])
 return result

For example, image A has 50% of pixels are black and 50% of pixels are white, image B has 100% pixels are black, then intersection = min(0.5, 1) + min(0.5, 0) = 0.5.

However, when we classify the images, it is hard to apply a single reference histogram to describe "luxury, indoor". Instead, we want to find the average similarity between a query histogram and a set of multiple reference histograms.

Typically, histograms are stored in sparse format. A sparse matrix contains mainly zeros. We will not store all the zeros individually, but instead store the ranges that are full of zeros.

OpenCV Pyramid LK

I have made the same mistake a thousand times so I think it is worth writing down.

error

error: ‘calcOpticalFlowPyrLK’ was not declared in this scope

solution according to this

#include <opencv2/video/tracking.hpp>

PCL with cmake

Here is a great tutorial about using PCL in cmake!

I use ROS indigo and I have no idea that it has its own PCL. So I blindly install another standalone PCL library. However, when I cmake the project, it gives me this error

undefined reference to pcl::PCDWriter

From this stackoverflow thread, it means we have to link libpcl_io.so in cmake. These are the changes I make

find_package(PCL REQUIRED)
change to
find_package(PCL REQUIRED COMPONENTS io)

and

target_link_libraries(img2pc ${catkin_LIBRARIES}  ${OpenCV_LIBRARIES} ${PCL_LIBRARY_DIRS})
to
target_link_libraries(img2pc ${catkin_LIBRARIES}  ${OpenCV_LIBRARIES} ${PCL_LIBRARY_DIRS} ${PCL_COMMON_LIBRARIES} ${PCL_IO_LIBRARIES})

I also add add_definitions(${PCL_DEFINITIONS})  in the end

The cmake could compile after making these changes.

Another thing to note when using eigen is that, there is no need to include it in cmake even if you call it in your code, ie #include <opencv2/core/eigen.hpp>

what we have to do according to this is to use #include <Eigen/Dense> at the beginning.

Algorithm - bipartite graph

Suppose we are playing in the universal studio, and we want to take the roller coaster. Each row only has two seats, and one female has to sit with a male. Everyone wants to sit with someone he/she knows. For example, if female 1 knows male 1, they can sit together. Those who know each other are female 1 (f1), male 1 (m1), (f1, m2), (f2, m2, m3), (f3, m1).

This kind of graph is called bipartite graph. The definition is: if the nodes in a graph can be divided into two groups, X and Y, and all the edges link one node in X and one node in Y. In other words, no edge link two nodes in X or Y.

We want to find the combination such that the total number of match is maximum.Start with f1. If she sits with m1, then f2 can sit with m2. However, f3 can only sit with m1, but m1 is sitting with f1.

To solve this problem, f3 asks m1 whether they can sit together. As a result, m1 asks f1 whether she can sit with other guys she knows. f1 then goes to m2, ans asks to sit together. m2 says: let me ask f2 whether she can find someone else. Eventually, f2 comes to m3, and since no one sits with him, they can sit together. Consequently, m2 can sit with f1, and m1 can sit with f3.

 

Reinstall ROS

I accidentally deleted cv_bridge when trying to compile the code for SLAM. I should have read the packages that will be deleted when I installed libjpeg in synaptics. 

Anyway, libjpeg destroys the cv_bridge package in my ROS Indigo. I could not install it back from synaptics either. 

The problem was solved by reinstall ROS Indigo, by the command from here. 

sudo apt-get install ros-indigo-desktop-full

How to use SSH key in Bitbucket

You could use SSH to avoid inputting password every time you push. Here are the steps of how to set up one with your bitbucket account in Ubantu.

Check that you do not already have a key
use sudo su to enter root
cd ~/.ssh
if it says bash: cd: /root/.ssh: No such file or directory, then you do not have a key
next, generate a key via ssh-keygen -t rsa
press enter at Enter file in which to save the key and Enter passphrase, just use default
your key will be saved in .ssh/id_rsa.pub
copy the content in .ssh/id_rsa.pub, gedit id_rsa.pub
to the manage account -> SSH keys in bitbucket
to test that you have valid connection, use ssh -T git@bitbucket.org, and enter yes
then you will see You can use git or hg to connect to Bitbucket. Shell access is disabled.

To use the key, you have to change the HTTP to SSH
use cat .git/config, you will see the url
edit the config file, accordingly

	SSH URL format	HTTPS URL format
Mercurial	ssh://hg@bitbucket.org/accountname/reponame/	https://accountname@bitbucket.org/accountname/reponame
Git	git@bitbucket.org:accountname/reponame.git or ssh://git@bitbucket.org/accountname/reponame.git	https://accountname@bitbucket.org/accountname/reponame.git

now you have to set chmod 400 ~/.ssh/id_rsa

then ssh-add ~/.ssh/id_rsa

Unfortunately, after all these hard work, my bitbucket still asks me for password. I use SmartGit instead, which is a GUI like sourceTree. Note that OpenJDK has to be installed beforehand in synaptic.

After all these mass, if you want to switch back to http, just delete the SSH stored in the bitbucket account.

浅谈MonoSLAM - 相机模型

最近读到一篇详细介绍MonoSLAM的thesis，这里稍作总结。

MonoSLAM只用了一个USB相机采集图像，所以作者从介绍相机模型开始。最简单的相机模型基于小孔成像。2D平面叫做pinhole plane，对应的3D坐标的原点叫做pinhole,也叫相机的optical center.3D坐标的三个坐标轴分别是$X_c, Y_c, Z_c$，分别指向右边，上边和前边。$Z_c$又叫optical axis或者principle axis.成像平面叫做image plane，跟pinhole plane平行，距离原点距离为f代表focal length，在$Z_c$的负半轴。$Z_c$轴和成像平面的交点叫做principle point或者image center，用R表示。


对于3D的点$P_i = (x_i,y_i,z_i)^T$，在图像中的坐标是$Q_i = (u_i,v_i)^T$。

虽然我们可以通过$P_i$坐标和f求得$(u_i,v_i)$，却不能反过来，用$(u_i,v_i)$和f求$P_i$，因为两点$P_i$和$P_j$都可以投影到同一个$(u_i,v_i)$，只要$\frac{x_i}{z_i} = \frac{x_j}{z_j}$, $\frac{y_i}{z_i} = \frac{y_j}{z_j}$.也就是说，对于$(u_i,v_i)$，所有在过原点和$(u_i,v_i)$的直线上的点都有可能是对应的3D坐标点。

为了进一步简化相机模型，我们通常使用virtual image plane.这个平面也平行于pinhole plane，不过在$Z_c$的正半轴上面，距离原点为f。这样就不用在图像坐标前面加负号了。在这个平面的投影叫做perspective projection.

对于真实的相机来说，小孔不能太小，否则通过的光线不足。另外，成像不是在image plane，而是在CCD/CMOS平面，有固定的大小，会影响field of view。感光元件的边界影响FOV的公式是

f是focal length，$U_{dim} \times V_{dim}$是感光元件的大小，$(\alpha_u, \alpha_v)$是FOV的角度。对于数码相机，公式也可以写作

$width \times height$表示图像的大小，$d_u, d_v$表示每一个像素对应的感光元件大小。
大部分相机的图像是320x240或者640x480.电脑程序一般以图像左上角作为原点，所以有

$o_u,o_v$代表左上角到中心的距离。+0.5是为了四舍五入。

现在问题来了，我们的相机目前只有2D信息，得不到3D点的深度。如果$P_i$在图像上的投影$Q_i = (u_i,v_i)^T$和f已知，那么$P_i$必然位于直线g上

为了得到3D信息，我们至少需要两张拍自不同地方的图片，才能使用triangulation.假设两个相机的pinhole plane共面，而且optical center之间的距离是b，或者说baseline是b，两个相机看向同一个方向。左边的相机和右边的相机分别用下标$l,r$表示。两个相机都观察同一点$P_i=(x_i,y_i,z_i)^T$，分别得到图像位置${Q_i}^l = ({u_i}^l,{v_i}^l)^T$和${Q_i}^r = ({u_i}^r,{v_i}^r)^T$。先假设${v_i}^l = {v_i}^r$。我们可以得到

$\Delta u_i$也叫做disparity。深度$z_i$跟disparity成反比。也就是说，如果disparity很大，很小的变化不会影响depth。反过来说，如果disparity接近0，一个小变化就会使得depth变化很大。距离相机越远的物体depth精度就越差。除了深度，通过triangulation也可以得到${x_i}^{\gamma},{y_i}^{\gamma}$

把两个相机想象成一个双目相机，optical center $O_c$在两个相机中间，我们可以得到变换后的2.25


把2.24中得到的$z_i$带入

对于每个相机，可以得到$P_i$所在的线，所以两个相机可以得到$g^l,g^r$的交点，也就是$P_i$的位置。除了双目相机，从移动的单目相机的两个不同位置$p^l,p^r$也可以得到深度。

补充
Opencv 3有个关于双目相机如何计算深度的图，在这里。结合这本书中的解释，(baseline - disparity) / baseline = (Z - f) / Z，注意xL = half image size + xL', xR = half image size - xR', 所以xL - xR = xL' + xR'。

Algorithm - queue, stack, node

Take an encryption case for example. You are given a sequence of number, 6 3 1 7 5 8 9 2 4, which is encrypted. To get the real meaning, we delete 6 and put 3 to the end, and the number becomes 1 7 5 8 9 2 4 3. Then we delete 1 and put 7 to the end, the number becomes 5 8 9 2 4 3 7. We delete 5 and put 8 to the end, getting 9 2 4 3 7 8... Eventually the numbers get deleted are 6 1 5 9 4 7 2 8 3.

Queue is a special structure, which only allows the elements at head to be deleted, which is called pop out. It only allows to input new elements at tail, means pop in. When head == tail, the queue is empty.

What is stack? Suppose we have a bucket, and we can only put in one ball each time. We now put in ball 2, 1, 3. If you want to take out ball 2, then you have to take ball 3 out first, and then ball 1.

We can use stack to determine whether a string is equal no matter if you read it forward or backward.

Now let's talk about node. We often use array to store numbers, but it is not always convenient. For example, we have a sequence of numbers, arranged in ascending order, 2 3 5 8 9 10 18 26 32. If we want to input 6 and ensure the new sequence is still in ascending order, then we have to move all the numbers after 8 if we use array.

What is node? Node is 2-3-5-8-9-10-18-26-32. If we want to input 6, we just need 2-3-5-6-8-9-10-18-26-32. Each node has two parts, one stores the data, using an int. The other stores the address of next data, using pointer.

An alternative way to realize node is to use array to simulate it. Suppose we have the data 2 3 5 8 9 10 18 26 32, we need to use another array called right to store the position of the number on the right of the data 2 3 4 5 6 7 8 9 0. For instance, right[1] = 2, means the number on the right of data[1] is in data[2]. right[9] = 0, means there is no number of the right of 9.

If we want to input 6, we only need to put it at the end, data[10] = 6. Then we need to change right[3] = 10, means we put the number on the right of data[3] to data[10]. We also need to set right[10] = 4, means the number right to data[10] is in data[4].

MonoSLAM for dummies

The basic idea about SLAM is that if I were a robot, and I know two fixed points: (x1, y1) and (x2, y2). I now can see point1, and the measurement tells me it is 5 m away from me. When I turn my head for 30 degrees, I can see point2, and the measurements tell me it is 10m away. As a result of knowing my relative position with respect to point1 and point2, I can localize myself.

But here comes the question. I have to look back to see point1 and point2 every time I move forward, to know where I am. This kind of looking back is very stupid. So, a smart PhD student comes up with a solution: as soon as I know where I am with respect to point1, point2, I add more points: point3, point4... because I know the coordinate of myself, I can measure the location of these points (mapping). I could use those points afterwards for localization.

Therefore, SLAM means knowing my localization and the coordinates of the fixed points (feature mapping). Because SLAM introduces noise no matter when measuring distance or calculating the rotation, traveled distance, SLAM requires Kalman filter.

MonoSLAM also refers to real time structure from motion. The fixed points are the visual features, and measuring distance becomes match feature and then triangulate.

MonoSLAM is implemented in MATLAB here. The authors introduce MonoSLAM in the following way. SLAM in a 3D environment - Need of 3D landmarks - Camera based method - use of visual 2D interest points - camera gives 2D interest points - no depth information - how to get depth? - by using camera motion - How to estimate camera motion - by using 3D landmarks.

Therefore, 3D landmark = 2D interest point + depth.

At the beginning, a few initial landmarks must be provided for initialization, otherwise the camera motion cannot be estimated. After the initialization phase, an iterative process begins. Step 1: 2D interest points must evolve into 3D landmarks when the estimate of their depth is good enough. Step 2: 3D landmarks contribute to the estimation of the state, including camera and the map.

The camera and map state is estimated through an EKF. After initialization, this filter performs a model based prediction, compares it to the measurements (camera data), and thus applies a correction on the global state according to the innovation.

To use camera data, we have to know its resolution, focal length, CMOS sensor dimension, and thus we need to perform a calibration step, such as the MATLAB toolbox.

The landmarks could be initialized manually, or by using an object of known size at the beginning.

Since we use EKF, we need to have a model, and the only model we can have for the camera is a kinematic one, instead of a dynamic one. This model allows only constant velocity movement. However, the camera may not move in this way. Hence we have to add a noise to allow for changes in direction or speed. This is necessary for the EKF to assess the confidence into its estimates.

A common noise model is the additive noise model, where random gaussian noise is added on each state component. But here we use a non linear, acceleration based noise model. To enable several trajectories around the previous one, we consider the linear and angular accelerations to be given by random zero mean gaussian variables. The standard deviation of these variables allows us to tune how uneven the motion can be.

The prediction step randomly chooses one trajectory among these possibilities, and if necessary the correction step will bring the system back in tracks.

Landmarks are identified from interest points. The Shi-Tomasi detector is used to define salient points. The detection is based on local extrema of the gradient analysis of 15x15 pixels patches. The eigenvalues of the matrix are used to assess the quality of a potential interest point, through a threshold. When a new interest point is identified, it is attached to its neighborhood, namely its 15x15 patch, to describe this point. The patch is normalized to increase the detection robustness for illumination change.

Since there is no depth information from a single image, we need to use motion to recover the depth. This is done using particle filter. When an interest point is selected, we only know that this point belongs to a certain line called the epipolar line. To estimate where the point lies on the epipolar line, the line is uniformly sampled by a given number of particles, where each particle represents a depth hypothesis. A maximal depth hypothesis related to the size of the environment limits the search zone.

When an interest point has been registered, meaning that its patch and epipolar line are known, the algorithm tries to match it in the subsequent pictures. An interest point without any depth information is tracked using correlation over a window. The size of the window is constant, defied by a maximal acceleration in terms of pixels. Interest points moving out of the image or weakly matched are discarded.

During the tracking, after the correlation has matched an interest point, all the particles associated to this point are re-projected in the picture. Resampling is performed to promote hypothesis best-linked to the correlation result, and 25% of the particles are resampled uniformly to avoid early convergence. When the variance of the depth hypotheses shrinks below a threshold, the estimation is considered reliable. The interest point is then attached a depth and becomes a landmark, with a large uncertainty along the epipolar line to allow the EKF to modify its position easily if necessary.

Compared to the interest point management (initialization, tracking, depth estimation and upgrade as landmark), landmark tracking is much easier. The EKF prediction gives an estimate of the camera position and orientation, as well as uncertainties on these quantities and on the landmarks position. The position and orientation of the camera, relative to the landmarks position, allow us to predict how the landmarks will be projected onto the image plane, along with an uncertainty area. Both the uncertainty of the camera position and orientation and the uncertainty of landmark position are taken into account to compute this uncertainty area. The larger the uncertainty is, the wider the search area is in the new picture. The the search is simply performed by correlation within this area. The difference between the EKF prediction and the camera observation gives the innovation signal of the filter.

When the algorithm is running, at least one landmark must always be visible. Thus, as soon as the number of visible landmarks falls below a chosen number, a search procedure is launched, in order to identify new interest points. This is achieved by searching interest points in randomly drawn windows. The only constraint on these windows is they have to be far away from the currently tracked landmarks and interest points. Otherwise, no effort is spent in trying to pick up interest points in the most useful place for the algorithm.

The innovation signal is at the core of the EKF correction step, which affects the whole state vector. We previously explained how the innovation signal is obtained, without any details concerning the projection.

The simple pinhole camera model is used to perform reprojection. No distortion correction is applied here. For a landmark yi described by its coordinates in the world frame, we have to express its position relatively to the camera.

Correction is based on the innovation. A simple additive noise is finally added to the observation model, which enables us to tune the confidence of the EKF towards the observations. To increase the robustness of the correction algorithm, landmarks weakly matched (bad correlation results) or unmatched (not seen when tey are predicted to be seen) along several frames are removed from the map. EKF is very likely to be lost if the landmark association is bad.

Reduce PDF size in Ubantu

According to this post, we can use Ghostscript to reduce the pdf size.

gs -sDEVICE=pdfwrite -dCompatibilityLevel=1.4 -dNOPAUSE -dQUIET -dBATCH -sOutputFile=foo-compressed.pdf foo.pdf

Latex table

In latex table, if you put \caption before \begin, then the caption will appear at the top. If you put \caption after \begin, the caption will appear below the table, which is the norm for most papers. Moreover, \label should be in the same line with \caption.

默写欧洲/英国的侦探们

一个景点的知名度往往能够从它对所在地的影响上面看出来。而大名鼎鼎的福尔摩斯博物馆更是从地铁站就开始了它的宣传。到达以福尔摩斯居住地命名的贝克街地铁站后，看到那里的仿古建筑，仿佛瞬间回到了大侦探所在的维多利亚时代。
 
 

带着这种穿越的感觉走出站口,激动的发现福尔摩斯本人就伫立在门口,叼着烟斗穿着斗篷和鹿皮帽子,仿佛正在思考着案件. 看到他的雕像,想必大多数福迷都会内心中无比的激动,心跳加速,面目通红,手舞足蹈,恨不得要个签名啥的.
 
福尔摩斯博物馆收费6英镑,平均每层2英镑,每个房间1.5英镑,估计是所有博物馆里面每层和每间房最贵的之一了.