MonoSLAM只用了一个USB相机采集图像,所以作者从介绍相机模型开始。最简单的相机模型基于小孔成像。2D平面叫做pinhole plane,对应的3D坐标的原点叫做pinhole,也叫相机的optical center.3D坐标的三个坐标轴分别是$X_c, Y_c, Z_c$,分别指向右边,上边和前边。$Z_c$又叫optical axis或者principle axis.成像平面叫做image plane,跟pinhole plane平行,距离原点距离为f代表focal length,在$Z_c$的负半轴。$Z_c$轴和成像平面的交点叫做principle point或者image center,用R表示。

对于3D的点$P_i = (x_i,y_i,z_i)^T$,在图像中的坐标是$Q_i = (u_i,v_i)^T$。
虽然我们可以通过$P_i$坐标和f求得$(u_i,v_i)$,却不能反过来,用$(u_i,v_i)$和f求$P_i$,因为两点$P_i$和$P_j$都可以投影到同一个$(u_i,v_i)$,只要$\frac{x_i}{z_i} = \frac{x_j}{z_j}$, $\frac{y_i}{z_i} = \frac{y_j}{z_j}$.也就是说,对于$(u_i,v_i)$,所有在过原点和$(u_i,v_i)$的直线上的点都有可能是对应的3D坐标点。
为了进一步简化相机模型,我们通常使用virtual image plane.这个平面也平行于pinhole plane,不过在$Z_c$的正半轴上面,距离原点为f。这样就不用在图像坐标前面加负号了。在这个平面的投影叫做perspective projection.

对于真实的相机来说,小孔不能太小,否则通过的光线不足。另外,成像不是在image plane,而是在CCD/CMOS平面,有固定的大小,会影响field of view。感光元件的边界影响FOV的公式是
f是focal length,$U_{dim} \times V_{dim}$是感光元件的大小,$(\alpha_u, \alpha_v)$是FOV的角度。对于数码相机,公式也可以写作
$width \times height$表示图像的大小,$d_u, d_v$表示每一个像素对应的感光元件大小。
大部分相机的图像是320x240或者640x480.电脑程序一般以图像左上角作为原点,所以有
$o_u,o_v$代表左上角到中心的距离。+0.5是为了四舍五入。
现在问题来了,我们的相机目前只有2D信息,得不到3D点的深度。如果$P_i$在图像上的投影$Q_i = (u_i,v_i)^T$和f已知,那么$P_i$必然位于直线g上
为了得到3D信息,我们至少需要两张拍自不同地方的图片,才能使用triangulation.假设两个相机的pinhole plane共面,而且optical center之间的距离是b,或者说baseline是b,两个相机看向同一个方向。左边的相机和右边的相机分别用下标$l,r$表示。两个相机都观察同一点$P_i=(x_i,y_i,z_i)^T$,分别得到图像位置${Q_i}^l = ({u_i}^l,{v_i}^l)^T$和${Q_i}^r = ({u_i}^r,{v_i}^r)^T$。先假设${v_i}^l = {v_i}^r$。我们可以得到
$\Delta u_i$也叫做disparity。深度$z_i$跟disparity成反比。也就是说,如果disparity很大,很小的变化不会影响depth。反过来说,如果disparity接近0,一个小变化就会使得depth变化很大。距离相机越远的物体depth精度就越差。除了深度,通过triangulation也可以得到${x_i}^{\gamma},{y_i}^{\gamma}$
把两个相机想象成一个双目相机,optical center $O_c$在两个相机中间,我们可以得到变换后的2.25

把2.24中得到的$z_i$带入
对于每个相机,可以得到$P_i$所在的线,所以两个相机可以得到$g^l,g^r$的交点,也就是$P_i$的位置。除了双目相机,从移动的单目相机的两个不同位置$p^l,p^r$也可以得到深度。
补充
Opencv 3有个关于双目相机如何计算深度的图,在这里。结合这本书中的解释,(baseline - disparity) / baseline = (Z - f) / Z,注意xL = half image size + xL', xR = half image size - xR', 所以xL - xR = xL' + xR'。
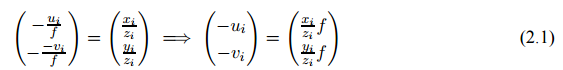











No comments:
Post a Comment